proporciones de un rectángulo deformado en perspectiva
Dada una imagen 2d de un rectángulo distorsionado por perspectiva:

Sé que la forma era originalmente un rectángulo, pero no sé su tamaño original.
Si conozco las coordenadas de píxeles de las esquinas de esta imagen, ¿cómo puedo calcular las proporciones originales, es decir, el cociente ( ancho / alto ) del rectángulo?
(fondo: el objetivo es eliminar automáticamente las fotos de documentos rectangulares, la detección de bordes probablemente se realizará con transformación de hough)
ACTUALIZACIÓN:
Ha habido alguna discusión sobre si es posible determinar la relación anchura:altura con la información dada. Mi ingenuo pensamiento fue que debe ser posible, ya que no se me ocurre ninguna manera de proyectar, por ejemplo, un rectángulo de 1:4 en el cuadrilátero representado arriba. La relación parece claramente cercana a 1: 1, por lo que debería haber una manera de determinarla matemáticamente. Sin embargo, no tengo pruebas de esto más allá de mi suposición intuitiva.
I todavía no han entendido completamente los argumentos presentados a continuación, pero creo que debe haber alguna suposición implícita de que estamos faltando aquí y que se interpreta de manera diferente.
Sin embargo, después de horas de búsqueda, finalmente he encontrado algunos documentos relevantes para el problema. Estoy luchando para entender las matemáticas utilizadas allí, hasta ahora sin éxito. En particular, el primer documento parece discutir exactamente lo que quería hacer, desafortunadamente sin ejemplos de código y muy denso matemáticas.
-
Zhengyou Zhang, Li-Wei He, " Escaneo de pizarra y mejora de imagen" http://research.microsoft.com/en-us/um/people/zhang/papers/tr03-39.pdf p. 11
"Debido a la distorsión de perspectiva, la imagen de un rectángulo parece ser un cuadrángulo. Sin embargo, como sabemos que es un rectángulo en el espacio, podemos estimar tanto la distancia focal de la cámara como la relación de aspecto del rectángulo."
-
ROBERT M. HARALICK " Determinación de parámetros de cámara desde la perspectiva proyección de un rectángulo"
http://portal.acm.org/citation.cfm?id=87146
"mostramos cómo utilizar la proyección en perspectiva 2D de un rectángulo de tamaño y posición desconocidos en el espacio 3D para determinar los parámetros del ángulo de aspecto de la cámara en relación con los planos del rectángulo."
10 answers
Aquí está mi intento de responder a mi pregunta después de leer el documento
- Zhengyou Zhang, Li-Wei He, "Escaneo de pizarra y mejora de imagen" http://research.microsoft.com/en-us/um/people/zhang/papers/tr03-39.pdf
Manipulé las ecuaciones durante algún tiempo en SAGE, y se me ocurrió este pseudo-código en estilo c:
// in case it matters: licensed under GPLv2 or later
// legend:
// sqr(x) = x*x
// sqrt(x) = square root of x
// let m1x,m1y ... m4x,m4y be the (x,y) pixel coordinates
// of the 4 corners of the detected quadrangle
// i.e. (m1x, m1y) are the cordinates of the first corner,
// (m2x, m2y) of the second corner and so on.
// let u0, v0 be the pixel coordinates of the principal point of the image
// for a normal camera this will be the center of the image,
// i.e. u0=IMAGEWIDTH/2; v0 =IMAGEHEIGHT/2
// This assumption does not hold if the image has been cropped asymmetrically
// first, transform the image so the principal point is at (0,0)
// this makes the following equations much easier
m1x = m1x - u0;
m1y = m1y - v0;
m2x = m2x - u0;
m2y = m2y - v0;
m3x = m3x - u0;
m3y = m3y - v0;
m4x = m4x - u0;
m4y = m4y - v0;
// temporary variables k2, k3
double k2 = ((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x) /
((m2y - m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) ;
double k3 = ((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y - m1y*m4x) /
((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) ;
// f_squared is the focal length of the camera, squared
// if k2==1 OR k3==1 then this equation is not solvable
// if the focal length is known, then this equation is not needed
// in that case assign f_squared= sqr(focal_length)
double f_squared =
-((k3*m3y - m1y)*(k2*m2y - m1y) + (k3*m3x - m1x)*(k2*m2x - m1x)) /
((k3 - 1)*(k2 - 1)) ;
//The width/height ratio of the original rectangle
double whRatio = sqrt(
(sqr(k2 - 1) + sqr(k2*m2y - m1y)/f_squared + sqr(k2*m2x - m1x)/f_squared) /
(sqr(k3 - 1) + sqr(k3*m3y - m1y)/f_squared + sqr(k3*m3x - m1x)/f_squared)
) ;
// if k2==1 AND k3==1, then the focal length equation is not solvable
// but the focal length is not needed to calculate the ratio.
// I am still trying to figure out under which circumstances k2 and k3 become 1
// but it seems to be when the rectangle is not distorted by perspective,
// i.e. viewed straight on. Then the equation is obvious:
if (k2==1 && k3==1) whRatio = sqrt(
(sqr(m2y-m1y) + sqr(m2x-m1x)) /
(sqr(m3y-m1y) + sqr(m3x-m1x))
// After testing, I found that the above equations
// actually give the height/width ratio of the rectangle,
// not the width/height ratio.
// If someone can find the error that caused this,
// I would be most grateful.
// until then:
whRatio = 1/whRatio;
Actualización: así es como se determinaron estas ecuaciones:
El siguiente es el código en SAGE. Puede ser accessed online at http://www.sagenb.org/home/pub/704 / . (Sage es realmente útil para resolver ecuaciones, y se puede usar en cualquier navegador, échale un vistazo)
# CALCULATING THE ASPECT RATIO OF A RECTANGLE DISTORTED BY PERSPECTIVE
#
# BIBLIOGRAPHY:
# [zhang-single]: "Single-View Geometry of A Rectangle
# With Application to Whiteboard Image Rectification"
# by Zhenggyou Zhang
# http://research.microsoft.com/users/zhang/Papers/WhiteboardRectification.pdf
# pixel coordinates of the 4 corners of the quadrangle (m1, m2, m3, m4)
# see [zhang-single] figure 1
m1x = var('m1x')
m1y = var('m1y')
m2x = var('m2x')
m2y = var('m2y')
m3x = var('m3x')
m3y = var('m3y')
m4x = var('m4x')
m4y = var('m4y')
# pixel coordinates of the principal point of the image
# for a normal camera this will be the center of the image,
# i.e. u0=IMAGEWIDTH/2; v0 =IMAGEHEIGHT/2
# This assumption does not hold if the image has been cropped asymmetrically
u0 = var('u0')
v0 = var('v0')
# pixel aspect ratio; for a normal camera pixels are square, so s=1
s = var('s')
# homogenous coordinates of the quadrangle
m1 = vector ([m1x,m1y,1])
m2 = vector ([m2x,m2y,1])
m3 = vector ([m3x,m3y,1])
m4 = vector ([m4x,m4y,1])
# the following equations are later used in calculating the the focal length
# and the rectangle's aspect ratio.
# temporary variables: k2, k3, n2, n3
# see [zhang-single] Equation 11, 12
k2_ = m1.cross_product(m4).dot_product(m3) / m2.cross_product(m4).dot_product(m3)
k3_ = m1.cross_product(m4).dot_product(m2) / m3.cross_product(m4).dot_product(m2)
k2 = var('k2')
k3 = var('k3')
# see [zhang-single] Equation 14,16
n2 = k2 * m2 - m1
n3 = k3 * m3 - m1
# the focal length of the camera.
f = var('f')
# see [zhang-single] Equation 21
f_ = sqrt(
-1 / (
n2[2]*n3[2]*s^2
) * (
(
n2[0]*n3[0] - (n2[0]*n3[2]+n2[2]*n3[0])*u0 + n2[2]*n3[2]*u0^2
)*s^2 + (
n2[1]*n3[1] - (n2[1]*n3[2]+n2[2]*n3[1])*v0 + n2[2]*n3[2]*v0^2
)
)
)
# standard pinhole camera matrix
# see [zhang-single] Equation 1
A = matrix([[f,0,u0],[0,s*f,v0],[0,0,1]])
#the width/height ratio of the original rectangle
# see [zhang-single] Equation 20
whRatio = sqrt (
(n2*A.transpose()^(-1) * A^(-1)*n2.transpose()) /
(n3*A.transpose()^(-1) * A^(-1)*n3.transpose())
)
Las ecuaciones simplificadas en el código c fueron determinadas por
print "simplified equations, assuming u0=0, v0=0, s=1"
print "k2 := ", k2_
print "k3 := ", k3_
print "f := ", f_(u0=0,v0=0,s=1)
print "whRatio := ", whRatio(u0=0,v0=0,s=1)
simplified equations, assuming u0=0, v0=0, s=1
k2 := ((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)/((m2y
- m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x)
k3 := ((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y - m1y*m4x)/((m3y
- m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x)
f := sqrt(-((k3*m3y - m1y)*(k2*m2y - m1y) + (k3*m3x - m1x)*(k2*m2x
- m1x))/((k3 - 1)*(k2 - 1)))
whRatio := sqrt(((k2 - 1)^2 + (k2*m2y - m1y)^2/f^2 + (k2*m2x -
m1x)^2/f^2)/((k3 - 1)^2 + (k3*m3y - m1y)^2/f^2 + (k3*m3x -
m1x)^2/f^2))
print "Everything in one equation:"
print "whRatio := ", whRatio(f=f_)(k2=k2_,k3=k3_)(u0=0,v0=0,s=1)
Everything in one equation:
whRatio := sqrt(((((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y -
m1y*m4x)/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) -
1)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)/((m2y -
m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) - 1)*(((m1y -
m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)*m2y/((m2y - m4y)*m3x
- (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) - m1y)^2/((((m1y - m4y)*m2x -
(m1x - m4x)*m2y + m1x*m4y - m1y*m4x)*m3y/((m3y - m4y)*m2x - (m3x -
m4x)*m2y + m3x*m4y - m3y*m4x) - m1y)*(((m1y - m4y)*m3x - (m1x -
m4x)*m3y + m1x*m4y - m1y*m4x)*m2y/((m2y - m4y)*m3x - (m2x - m4x)*m3y
+ m2x*m4y - m2y*m4x) - m1y) + (((m1y - m4y)*m2x - (m1x - m4x)*m2y +
m1x*m4y - m1y*m4x)*m3x/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y
- m3y*m4x) - m1x)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y -
m1y*m4x)*m2x/((m2y - m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x)
- m1x)) + (((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y -
m1y*m4x)/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) -
1)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)/((m2y -
m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) - 1)*(((m1y -
m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)*m2x/((m2y - m4y)*m3x
- (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) - m1x)^2/((((m1y - m4y)*m2x -
(m1x - m4x)*m2y + m1x*m4y - m1y*m4x)*m3y/((m3y - m4y)*m2x - (m3x -
m4x)*m2y + m3x*m4y - m3y*m4x) - m1y)*(((m1y - m4y)*m3x - (m1x -
m4x)*m3y + m1x*m4y - m1y*m4x)*m2y/((m2y - m4y)*m3x - (m2x - m4x)*m3y
+ m2x*m4y - m2y*m4x) - m1y) + (((m1y - m4y)*m2x - (m1x - m4x)*m2y +
m1x*m4y - m1y*m4x)*m3x/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y
- m3y*m4x) - m1x)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y -
m1y*m4x)*m2x/((m2y - m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x)
- m1x)) - (((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y -
m1y*m4x)/((m2y - m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) -
1)^2)/((((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y -
m1y*m4x)/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) -
1)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)/((m2y -
m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) - 1)*(((m1y -
m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y - m1y*m4x)*m3y/((m3y - m4y)*m2x
- (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) - m1y)^2/((((m1y - m4y)*m2x -
(m1x - m4x)*m2y + m1x*m4y - m1y*m4x)*m3y/((m3y - m4y)*m2x - (m3x -
m4x)*m2y + m3x*m4y - m3y*m4x) - m1y)*(((m1y - m4y)*m3x - (m1x -
m4x)*m3y + m1x*m4y - m1y*m4x)*m2y/((m2y - m4y)*m3x - (m2x - m4x)*m3y
+ m2x*m4y - m2y*m4x) - m1y) + (((m1y - m4y)*m2x - (m1x - m4x)*m2y +
m1x*m4y - m1y*m4x)*m3x/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y
- m3y*m4x) - m1x)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y -
m1y*m4x)*m2x/((m2y - m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x)
- m1x)) + (((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y -
m1y*m4x)/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) -
1)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y - m1y*m4x)/((m2y -
m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x) - 1)*(((m1y -
m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y - m1y*m4x)*m3x/((m3y - m4y)*m2x
- (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) - m1x)^2/((((m1y - m4y)*m2x -
(m1x - m4x)*m2y + m1x*m4y - m1y*m4x)*m3y/((m3y - m4y)*m2x - (m3x -
m4x)*m2y + m3x*m4y - m3y*m4x) - m1y)*(((m1y - m4y)*m3x - (m1x -
m4x)*m3y + m1x*m4y - m1y*m4x)*m2y/((m2y - m4y)*m3x - (m2x - m4x)*m3y
+ m2x*m4y - m2y*m4x) - m1y) + (((m1y - m4y)*m2x - (m1x - m4x)*m2y +
m1x*m4y - m1y*m4x)*m3x/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y
- m3y*m4x) - m1x)*(((m1y - m4y)*m3x - (m1x - m4x)*m3y + m1x*m4y -
m1y*m4x)*m2x/((m2y - m4y)*m3x - (m2x - m4x)*m3y + m2x*m4y - m2y*m4x)
- m1x)) - (((m1y - m4y)*m2x - (m1x - m4x)*m2y + m1x*m4y -
m1y*m4x)/((m3y - m4y)*m2x - (m3x - m4x)*m2y + m3x*m4y - m3y*m4x) -
1)^2))
# some testing:
# - choose a random rectangle,
# - project it onto a random plane,
# - insert the corners in the above equations,
# - check if the aspect ratio is correct.
from sage.plot.plot3d.transform import rotate_arbitrary
#redundandly random rotation matrix
rand_rotMatrix = \
rotate_arbitrary((uniform(-5,5),uniform(-5,5),uniform(-5,5)),uniform(-5,5)) *\
rotate_arbitrary((uniform(-5,5),uniform(-5,5),uniform(-5,5)),uniform(-5,5)) *\
rotate_arbitrary((uniform(-5,5),uniform(-5,5),uniform(-5,5)),uniform(-5,5))
#random translation vector
rand_transVector = vector((uniform(-10,10),uniform(-10,10),uniform(-10,10))).transpose()
#random rectangle parameters
rand_width =uniform(0.1,10)
rand_height=uniform(0.1,10)
rand_left =uniform(-10,10)
rand_top =uniform(-10,10)
#random focal length and principal point
rand_f = uniform(0.1,100)
rand_u0 = uniform(-100,100)
rand_v0 = uniform(-100,100)
# homogenous standard pinhole projection, see [zhang-single] Equation 1
hom_projection = A * rand_rotMatrix.augment(rand_transVector)
# construct a random rectangle in the plane z=0, then project it randomly
rand_m1hom = hom_projection*vector((rand_left ,rand_top ,0,1)).transpose()
rand_m2hom = hom_projection*vector((rand_left ,rand_top+rand_height,0,1)).transpose()
rand_m3hom = hom_projection*vector((rand_left+rand_width,rand_top ,0,1)).transpose()
rand_m4hom = hom_projection*vector((rand_left+rand_width,rand_top+rand_height,0,1)).transpose()
#change type from 1x3 matrix to vector
rand_m1hom = rand_m1hom.column(0)
rand_m2hom = rand_m2hom.column(0)
rand_m3hom = rand_m3hom.column(0)
rand_m4hom = rand_m4hom.column(0)
#normalize
rand_m1hom = rand_m1hom/rand_m1hom[2]
rand_m2hom = rand_m2hom/rand_m2hom[2]
rand_m3hom = rand_m3hom/rand_m3hom[2]
rand_m4hom = rand_m4hom/rand_m4hom[2]
#substitute random values for f, u0, v0
rand_m1hom = rand_m1hom(f=rand_f,s=1,u0=rand_u0,v0=rand_v0)
rand_m2hom = rand_m2hom(f=rand_f,s=1,u0=rand_u0,v0=rand_v0)
rand_m3hom = rand_m3hom(f=rand_f,s=1,u0=rand_u0,v0=rand_v0)
rand_m4hom = rand_m4hom(f=rand_f,s=1,u0=rand_u0,v0=rand_v0)
# printing the randomly choosen values
print "ground truth: f=", rand_f, "; ratio=", rand_width/rand_height
# substitute all the variables in the equations:
print "calculated: f= ",\
f_(k2=k2_,k3=k3_)(s=1,u0=rand_u0,v0=rand_v0)(
m1x=rand_m1hom[0],m1y=rand_m1hom[1],
m2x=rand_m2hom[0],m2y=rand_m2hom[1],
m3x=rand_m3hom[0],m3y=rand_m3hom[1],
m4x=rand_m4hom[0],m4y=rand_m4hom[1],
),"; 1/ratio=", \
1/whRatio(f=f_)(k2=k2_,k3=k3_)(s=1,u0=rand_u0,v0=rand_v0)(
m1x=rand_m1hom[0],m1y=rand_m1hom[1],
m2x=rand_m2hom[0],m2y=rand_m2hom[1],
m3x=rand_m3hom[0],m3y=rand_m3hom[1],
m4x=rand_m4hom[0],m4y=rand_m4hom[1],
)
print "k2 = ", k2_(
m1x=rand_m1hom[0],m1y=rand_m1hom[1],
m2x=rand_m2hom[0],m2y=rand_m2hom[1],
m3x=rand_m3hom[0],m3y=rand_m3hom[1],
m4x=rand_m4hom[0],m4y=rand_m4hom[1],
), "; k3 = ", k3_(
m1x=rand_m1hom[0],m1y=rand_m1hom[1],
m2x=rand_m2hom[0],m2y=rand_m2hom[1],
m3x=rand_m3hom[0],m3y=rand_m3hom[1],
m4x=rand_m4hom[0],m4y=rand_m4hom[1],
)
# ATTENTION: testing revealed, that the whRatio
# is actually the height/width ratio,
# not the width/height ratio
# This contradicts [zhang-single]
# if anyone can find the error that caused this, I'd be grateful
ground truth: f= 72.1045134124554 ; ratio= 3.46538779959142
calculated: f= 72.1045134125 ; 1/ratio= 3.46538779959
k2 = 0.99114614987 ; k3 = 1.57376280159
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2009-08-03 21:27:12
Update
Después de leer su actualización y mirar la primera referencia (escaneo de pizarra y mejora de imagen), veo dónde está el punto que falta.
Los datos de entrada del problema son un cuádruple (A,B,C,D), Y el centro O de la imagen proyectada. En el artículo, corresponde a la suposición u0 = v0 = 0. Añadiendo este punto, el problema se vuelve lo suficientemente restringido como para obtener la relación de aspecto del rectángulo.
El problema se vuelve a plantear como sigue: Dado un cuádruple (A,B,C, D) en el plano Z=0,encuentre la posición del ojo E(0,0, h), h>0 y un plano 3D P tal que la proyección de (A,B,C, D) en P sea un rectángulo.
Tenga en cuenta que P está determinada por E: para obtener un paralelogramo, P debe contener paralelos a (EU) y (EV), donde U=(AB)x(CD) y V=(AD)x(BC).
Experimentalmente, parece que este problema tiene en general una solución única, correspondiente a un valor único de la relación p/h de la rectángulo.
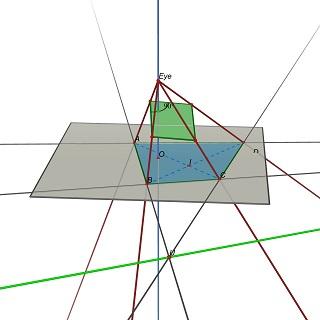
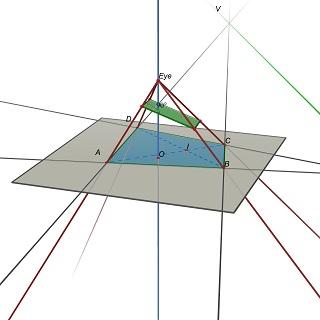
Mensaje anterior
No, no se puede determinar la relación del rectángulo a partir de la proyección.
En el caso general, una cuádruple (A,B,C,D) de cuatro puntos no colineales del plano Z=0 es la proyección de infinitos rectángulos, con infinitos ratios de anchura/altura.
Considere los dos puntos de fuga U, intersección de (AB) y (CD) y V, intersección de (AD) y (BC), y el punto I, intersección de los dos diagonales (AC) y (BD). Para proyectar como ABCD, un paralelogramo de centro I debe estar en un plano que contiene la línea paralela a (UV) a través del punto I. En uno de estos planos, se pueden encontrar muchos rectángulos que se proyectan a ABCD, todos con una relación w/h diferente.
Vea estas dos imágenes hechas con Cabri 3D. En los dos casos ABCD no cambia (en el plano gris Z=0), y el plano azul que contiene el rectángulo tampoco cambia. La línea verde parcialmente oculta es la línea (UV) y el verde visible la línea es paralela a ella y contiene I.
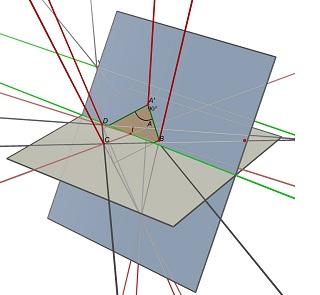
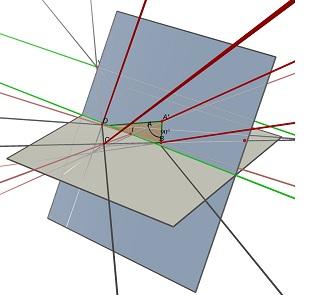
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2015-06-20 02:06:48
El tamaño no es realmente necesario, y tampoco lo son las proporciones. Y saber de qué lado está es irrelevante considerando que está usando fotos/escaneos de documentos. Dudo que vaya a escanear la parte trasera de ellos.
"Intersección de esquina" es el método para corregir la perspectiva. Esto podría ser de ayuda:
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2017-05-23 12:25:03
Sobre la cuestión de por qué los resultados dan h / w en lugar de w / h: Me pregunto si la expresión de la ecuación 20 anterior es correcta. Publicado es:
whRatio = sqrt (
(n2*A.transpose()^(-1) * A^(-1)*n2.transpose()) /
(n3*A.transpose()^(-1) * A^(-1)*n3.transpose())
)
Cuando intento ejecutar eso con OpenCV, obtengo una excepción. Pero todo funciona correctamente cuando uso la siguiente ecuación que para mí se parece más a la Ecuación 20: Pero basado en la Ecuación 20, parece que debería ser:
whRatio = sqrt (
(n2.transpose()*A.transpose()^(-1) * A^(-1)*n2) /
(n3.transpose()*A.transpose()^(-1) * A^(-1)*n3)
)
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2012-03-14 09:28:23
Puede determinar el ancho / alto con esta respuesta Calculando la coordenada 3D del rectángulo con la coordenada de su sombra?. Suponga que su rectángulo gire en el punto diagonal de intersección calcule su ancho y alto. Pero cuando cambia la distancia entre el plano de sombra de asunción al plano de sombra real proporcional del rectángulo es el mismo con el ancho / alto calculado!
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2017-05-23 12:09:12
Es imposible conocer el ancho de este rectángulo sin conocer la distancia de la 'cámara'.
Un pequeño rectángulo visto desde 5 centímetros de distancia se ve igual que un rectángulo enorme visto desde metros de distancia
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2009-07-28 14:31:51
Dibuja un triángulo isósceles derecho con esos dos puntos de fuga y un tercer punto debajo del horizonte (es decir, en el mismo lado del horizonte que está el rectángulo). Ese tercer punto será nuestro origen y las dos líneas a los puntos de fuga serán nuestros ejes. Llame a la distancia desde el origen a un punto de fuga pi/2. Ahora extienda los lados del rectángulo desde los puntos de fuga hasta los ejes, y marque dónde se cruzan los ejes. Elija un eje, medir las distancias de los dos las marcas al origen, transforman esas distancias: x- > tan (x), y la diferencia será la longitud "verdadera" de ese lado. Haga lo mismo para el otro eje. Toma la proporción de esas dos longitudes y listo.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2009-07-28 23:51:38
Necesita más información, esa figura transformada podría provenir de cualquier paralelogramo dada una perspectiva arbitraria.
Así que supongo que primero necesitas hacer algún tipo de calibración.
Edit: para aquellos que dijeron que estaba equivocado, aquí va la prueba matemática de que hay infinitas combinaciones de rectángulos / cámaras que ceden a la misma proyección:
Para simplificar el problema (ya que solo necesitamos la relación de los lados) asumamos que nuestro rectángulo está definido por los siguientes puntos: R=[(0,0),(1,0),(1,r),(0,r)] (esta simplificación es la misma que transformar cualquier problema en uno equivalente en un espacio afín).
El polígono transformado se define como: T=[(tx0,ty0),(tx1,ty1),(tx2,ty2),(tx3,ty3)]
Existe una matriz de transformación M = [[m00,m01,m02],[m10,m11,m12],[m20,m21,m22]] que satisface (Rxi,Ryi,1)*M=wi(txi,tyi,1)'
Si expandimos la ecuación anterior para los puntos,
Para R_0 obtenemos: m02-tx0*w0 = m12-ty0*w0 = m22-w0 = 0
Para R_1 obtenemos: m00-tx1*w1 = m10-ty1*w1 = m20+m22-w1 = 0
Para R_2 obtenemos: m00+r*m01-tx2*w2 = m10+r*m11-ty2*w2 = m20+r*m21+m22-w2 = 0
Y para R_3 nosotros obtener: m00+r*m01-tx3*w3 = m10+r*m11-ty3*w3 = m20 + r*m21 + m22 -w3 = 0
Hasta el momento tenemos 12 ecuaciones, 14 variables desconocidas (9 de la matriz, 4 de la wi, y 1 para la relación r) y el resto son valores conocidos (txi y tyi se dan).
Incluso si el sistema no estuviera subespecificado, algunas de las incógnitas se multiplican entre sí (r y mi0 productos) haciendo que el sistema no sea lineal (podría transformarlo en un sistema lineal asignando un nuevo nombre a cada producto, pero terminará aún con 13 incógnitas, y 3 de se expanden a soluciones infinitas).
Si usted puede encontrar cualquier defecto en el razonamiento o las matemáticas, por favor hágamelo saber.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2009-07-29 17:40:52
Dropbox tiene un extenso artículo en su blog de tecnología donde describen cómo resolvieron el problema de su aplicación de escáner.
Https://blogs.dropbox.com/tech/2016/08/fast-document-rectification-and-enhancement/
Rectificar un documento
Asumimos que el documento de entrada es rectangular en el mundo físico, pero si no está exactamente frente a la cámara, las esquinas resultantes en la imagen serán un cuadrilátero convexo general. Para satisfacer nuestro primer objetivo, debemos deshacer la transformación geométrica aplicada por el proceso de captura. Esta transformación depende del punto de vista de la cámara en relación con el documento (estos son los llamados parámetros extrínsecos), además de cosas como la distancia focal de la cámara (los parámetros intrínsecos). Aquí hay un diagrama del escenario de captura:
Para deshacer la transformación geométrica, primero debemos determinar dichos parámetros. Si asumimos una cámara bien simétrica (no astigmatismo, sin sesgo, etcétera), las incógnitas en este modelo son:
- la ubicación 3D de la cámara en relación con el documento (3 grados de libertad),
- la orientación 3D de la cámara en relación con el documento (3 grados de libertad),
- las dimensiones del documento (2 grados de libertad), y
- la distancia focal de la cámara (1 grado de libertad).
Por otro lado, las coordenadas x e y de los cuatro documentos detectados esquinas nos da efectivamente ocho restricciones. Aunque aparentemente hay más incógnitas (9) que restricciones (8), las incógnitas no son variables totalmente libres-uno podría imaginar escalar el documento físicamente y colocarlo más lejos de la cámara, para obtener una foto idéntica. Esta relación pone una restricción adicional, por lo que tenemos un sistema totalmente restringido que resolver. (El sistema real de ecuaciones que resolvemos implica algunas otras consideraciones; el artículo relevante de Wikipedia da una buen resumen: https://en.wikipedia.org/wiki/Camera_resectioning)
Una vez recuperados los parámetros, podemos deshacer la transformación geométrica aplicada por el proceso de captura para obtener una bonita imagen rectangular. Sin embargo, este es potencialmente un proceso que consume mucho tiempo: uno buscaría, para cada píxel de salida, el valor del píxel de entrada correspondiente en la imagen de origen. Por supuesto, las GPU están diseñadas específicamente para tareas como esta: renderizar una textura en un espacio virtual. Existe una transformación de vista, que resulta ser la inversa de la transformación de cámara que acabamos de resolver.- con el que se puede renderizar la imagen de entrada completa y obtener el documento rectificado. (Una manera fácil de ver esto es tener en cuenta que una vez que tenga la imagen de entrada completa en la pantalla de su teléfono, puede inclinar y traducir el teléfono de manera que la proyección de la región del documento en la pantalla le parezca rectilínea.)
Por último, recordemos que había una ambigüedad con respecto a escala: no podemos decir si el documento era un papel tamaño carta (8.5" x 11") o una cartulina (17" x 22"), por ejemplo. ¿Cuáles deben ser las dimensiones de la imagen de salida? Para resolver esta ambigüedad, contamos el número de píxeles dentro del cuadrilátero en la imagen de entrada y establecemos la resolución de salida para que coincida con este número de píxeles. La idea es que no queremos aumentar o disminuir la imagen demasiado.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2017-01-12 20:32:18
Parece que todavía hay cierta confusión sobre este interesante problema. Quiero dar una explicación fácil de seguir para cuando el problema puede y no puede ser resuelto.
Restricciones y Grados de Libertad
Normalmente, cuando nos enfrentamos a un problema como este, lo primero que debemos hacer es evaluar el número de Grados de Libertad desconocidos (DoFs) N, y el número de ecuaciones independientes M que tenemos para restringir los DoFs desconocidos. Es imposible resolver el problema si N si excede M (lo que significa que hay menos restricciones que incógnitas). Podemos descartar todos los problemas donde este es el caso como irresolubles. Si N no excede M entonces puede ser posible resolver el problema con una solución única, pero esto no está garantizado (ver el penúltimo párrafo para un ejemplo).
Usemos p1, p2, p 3 and p 4 to denote the positions of the 4 corners of the planar surface in world coordinates. Usemos R y t para ser la rotación y traducción 3D que las transforma en coordenadas de cámara. Usemos K para denotar la matriz intrínseca de la cámara 3x3. Ignoraremos la distorsión de la lente por ahora. La posición 2D de la ith esquina en la imagen de la cámara está dada por pi=f(K(Rpi+t)), donde f es la proyección de la función f(x,y,z)=(x/z,y/z). Usando esta ecuación sabemos que cada esquina en la imagen nos da dos ecuaciones (es decir, dos restricciones) en nuestras incógnitas: una del componente x de qi y una del componente y. Así que tenemos un total de 8 restricciones para trabajar. El nombre oficial de estas restricciones son las restricciones de reproyección .
Entonces, ¿cuáles son nuestros DoFs desconocidos? Ciertamente R y t son desconocidos, porque no sabemos la cámara pose de coordenadas del mundo. Por lo tanto, ya tenemos 6 DoFs desconocidos: 3 para R (por ejemplo, guiñada, cabeceo y balanceo) y 3 para t . Por lo tanto, no puede haber un máximo de dos incógnitas en el resto de los términos (K, p1, p2, p3, p4).
Diferentes problemas
Podemos construir diferentes problemas de la función en la que los dos términos en (K, p1, p2, p3, p4) vamos a considerar como desconocido. En este punto vamos a escribir K en la forma habitual: K=(fx, 0, cx; 0, fy, cy; 0,0,1) donde fx y fy son los términos de distancia focal (fx / fy normalmente se llama la relación de aspecto de la imagen) y (cx,cy) es el punto principal (el centro de proyección en la imagen).
Podríamos obtener un problema por tener fx y fy como nuestros dos incógnitas, y asumir (cx, cy, p1, p2, p3, p4) son conocidos. De hecho, este mismo problema se utiliza y resuelve dentro del método de calibración de la cámara de OpenCV, utilizando imágenes de un objetivo plano de tablero de ajedrez. Esto se utiliza para obtener una inicial estimación para fx y fy, asumiendo que el punto principal está en el centro de la imagen (que es una suposición muy razonable para la mayoría de las cámaras).
Alternativamente podemos crear un problema diferente asumiendo fx=fy, que de nuevo es bastante razonable para muchas cámaras, y asumir que esta distancia focal (denotada como f) es la solo desconocida en K. Por lo tanto, todavía nos queda una incógnita para jugar (recordemos que podemos tener un máximo de dos incógnitas). Así que vamos a utilizar esto suponiendo que conocido la forma del plano: como un rectángulo (que era la suposición original en la pregunta). Por lo tanto, podemos definir las esquinas de la siguiente manera: p1=(0,0,0), p2=(0,w,0), p3=(h,0,0) y p4=(h,w,0), donde h y w denota la altura y el ancho del rectángulo. Ahora, debido a que solo nos queda 1 desconocido, vamos a establecer esto como la relación de aspecto del plano: x = w / h. Ahora la pregunta es podemos recuperar simultáneamente x, f, R y t desde el 8 ¿restricciones de reproyección? ¡La respuesta es sí! Y la solución se da en el documento de Zhang citado en la pregunta.
La ambigüedad de la escala
Uno podría preguntarse si se puede resolver otro problema: si asumimos que K es conocido y las 2 incógnitas son h y w. ¿Se pueden resolver a partir de las ecuaciones de reproyección? La respuesta es no, y es porque hay una ambigüedad entre el tamaño del plano y la profundidad del plano a la cámara. Específicamente si escalamos el esquinas pi por s y escala t por s, luego s cancela en las ecuaciones de reproyección. Por lo tanto, la escala absoluta del plano no es recuperable.
Puede haber otros problemas con diferentes combinaciones para los DOF desconocidos, por ejemplo tener R, t , uno de los componentes principales del punto y el ancho del plano"s como incógnitas. Sin embargo, hay que pensar en qué casos son de utilidad práctica. Sin embargo, todavía no he visto un conjunto sistemático de soluciones para todas las combinaciones útiles!
Más puntos
Podríamos pensar que si añadiéramos correspondencias de puntos extra entre el plano y la imagen, o explotáramos los bordes del plano, podríamos recuperar más de 8 DOF desconocidos. Lamentablemente la respuesta es no. Esto se debe a que no agregan ninguna restricción independiente adicional. La razón es porque las 4 esquinas describen completamente la transformación del plano a la imagen. Esto se puede ver ajustando una matriz de homografía usando las cuatro esquinas, que luego pueden determinar las posiciones de todos los demás puntos en el plano en la imagen.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2018-01-16 20:30:56