Programación de clases a satisfacibilidad booleana [Reducción de tiempo polinómico]
Tengo algún problema teórico / práctico y no tengo ni idea por ahora de cómo manejarlo, aquí está:
Creo un solucionador SATcapaz de encontrar un modelo cuando ya existe y probar la contradicción cuando no es el caso en CNF problemas en C usando algoritmos genéticos.
Un problema SAT se parece básicamente a este tipo de problema :
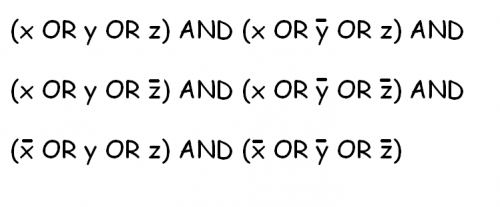 Mi objetivo es usar este solucionador para encontrar soluciones en muchos problemas NP-completes diferentes. Básicamente, traduzco diferentes problemas en SAT, resuelvo SAT con mi solucionador y luego transformo la solución en una solución aceptable para el problema original.
Mi objetivo es usar este solucionador para encontrar soluciones en muchos problemas NP-completes diferentes. Básicamente, traduzco diferentes problemas en SAT, resuelvo SAT con mi solucionador y luego transformo la solución en una solución aceptable para el problema original.
Ya tengo éxito para el Sudoku N*N y también para los problemas de N-queens, pero aquí está mi nuevo objetivo : reducir el Problema de Programación de Clases a SAT, pero no tengo idea de cómo formalizar un problema de programación de clases para transformarlo fácilmente en SAT después.
El objetivo es obviamente, en pocos meses, generar una imagen de un horario como este:

Encontré este código fuente que es capaz de resolver la programación de clases pero sin ninguna reducción a SAT desafortunadamente: /
También encontré algunos artículos sobre Planificación en general ( http://www.cs.rochester.edu/users/faculty/kautz/papers/kautz-satplan06.pdf por ejemplo).
Pero el lenguaje de definición de dominio de planificación utilizado en este artículo parece demasiado general para mí para representar un Problema de programación de clases. :/
¿Alguien tiene una idea sobre cómo formalizar eficientemente una programación de clases para reducirla a SAT y después, transformar la solución SAT (si existe ^^) en una programación de clases ?
Básicamente estoy abierto a cualquier sugerencia, por ahora no tengo idea de cómo representar, cómo reducir el problema, cómo transformar la solución SAT en un horario...
Pregunta de seguimiento: Programación de Clases a Booleano satisfacibilidad [Reducción del tiempo polinómico] parte 2
1 answers
Voy a tratar de formalizar primero el problema, y luego intentar reducirlo a SAT.
Defina el problema de programación de clases como:
Input = { S1,S2,....,Sn | Si = {(x_i1, y_i1), (x_i2, y_i2) , ... , (x_ik, y_ik) | 0 <= x_ij < y_ij <= M } }
Informalmente: La entrada es un conjunto de clases, cada clase es un conjunto de intervalos (abiertos) en la forma (x,y)
(M es una constante que describe el "final de la semana")
Salida: True si y solo si existe algún conjunto:
R = { (x_1j1, y_1j1) , ..., (x_njn, y_njn) | for each a,b: (x_aja,y_aja) INTERSECTION (x_bjb,y_bjb) = {} }
Informalmente: verdadero si y solo si hay alguna asignación de intervalos tales que la intersección entre cada par de intervalos está vacía.
Reducción a SAT:
Define una variable booleana para cada intervalo, V_ij
Basado en ella, defina la fórmula:
F1 = (V_11 OR V_12 OR ... OR V_1(k_1)) AND .... AND (V_n1 OR V_n2 OR ... OR V_n(k_n))
Informalmente, F1 se satisface si y solo si al menos uno de los intervalos para cada clase está "satisfecho"
Define Smaller(x,y) = true si y solo if x <= y1
Lo usaremos para asegurarnos de que los intervalos no se superpongan.
Tenga en cuenta que si queremos para asegurarnos de que (x1,y1) y (x2,y2) no se superpongan, necesitamos:
x1 <= y1 <= x2 <= y2 OR x2 <= y2 <= x1 <= y1
Dado que la entrada garantiza x1<=y1, x2<=y2, se reduce a:
y1<= x2 OR y2 <= x1
Y usando nuestras cláusulas más pequeñas y booleanas:
Smaller(y1,x2) OR Smaller(y2,x1)
Ahora, vamos a definir nuevas cláusulas para manejar con él:
Para cada par de clases a,b e intervalos c, d en ellos (c en a, d en b)
G_{c,d} = (Not(V_ac) OR Not(V_bd) OR Smaller(y_ac,x_bd) OR Smaller(y_bd,x_ac))
Informalmente, si uno de los intervalos b o d no se utiliza - la cláusula se cumple y hemos terminado. De lo contrario, ambos se utilizan, y debe asegurarse de que no haya solapamiento entre los dos intervalos.
Esto garantiza que si ambos c,d son "elegidos" - no se superponen, y esto es cierto para cada par de intervalos.
Ahora, formemos nuestra fórmula final: {[18]]}
F = F1 AND {G_{c,d} | for each c,d}
Esta fórmula nos asegura:
- Para cada clase, se elige al menos un intervalo
- Para cada dos intervalos c,d - si se eligen ambos c y d, no se superponen.
Pequeña nota: Esta fórmula permite elegir más de 1 intervalo de cada clase, pero si hay una solución con algunos intervalos t>1, puede eliminar fácilmente t - 1 de ellos sin cambiar la corrección de la solución.
Al final, los intervalos elegidos son las variables booleanas V_ij que definimos.
Ejemplo:
Alebgra = {(1,3),(3,5),(4,6)} Calculus = {(1,4),(2,5)}
Define F:
F1 = (V1,1 OR V1,2 OR V1,3) AND (V2,1 OR V2,2)
Definir G's:
G{A1,C1} = Not(V1,1) OR Not(V2,1) OR 4 <= 1 OR 3 <= 1 //clause for A(1,3) C(1,4)
= Not(V1,1) OR Not(V2,1) OR false =
= Not(V1,1) OR Not(V2,1)
G{A1,C2} = Not(V1,1) OR Not(V2,2) OR 3 <= 2 OR 5 <= 1 // clause for A(1,3) C(2,5)
= Not(V1,1) OR Not(V2,2) OR false =
= Not(V1,1) OR Not(V2,2)
G{A2,C1} = Not(V1,2) OR Not(V2,1) OR 5 <= 1 OR 4 <= 3 //clause for A(3,5) C(1,4)
= Not(V1,2) OR Not(V2,1) OR false =
= Not(V1,2) OR Not(V2,1)
G{A2,C2} = Not(V1,2) OR Not(V2,2) OR 5 <= 2 OR 5 <= 3 // clause for A(3,5) C(2,5)
= Not(V1,2) OR Not(V2,2) OR false =
= Not(V1,2) OR Not(V2,2)
G{A3,C1} = Not(V1,3) OR Not(V2,1) OR 4 <= 4 OR 6 <= 1 //clause for A(4,6) C(1,4)
= Not(V1,3) OR Not(V2,1) OR true=
= true
G{A3,C2} = Not(V1,3) OR Not(V2,2) OR 6 <= 2 OR 5 <= 4 // clause for A(4,6) C(2,5)
= Not(V1,3) OR Not(V2,2) OR false =
= Not(V1,3) OR Not(V2,2)
Ahora podemos mostrar nuestra fórmula final:
F = (V1,1 OR V1,2 OR V1,3) AND (V2,1 OR V2,2)
AND Not(V1,1) OR Not(V2,1) AND Not(V1,1) OR Not(V2,2)
AND Not(V1,2) OR Not(V2,1) AND Not(V1,2) OR Not(V2,2)
AND true AND Not(V1,3) OR Not(V2,2)
Lo anterior se cumple solo cuando:
V1,1 = false
V1,2 = false
V1,3 = true
V2,1 = true
V2,2 = false
, Y que se para el horario: Álgebra=(4,6); Cálculo=(1,4), como se desee.
(1) se puede calcular como una constante a la fórmula con bastante facilidad, hay un número polinómico de tales constantes.
Warning: date(): Invalid date.timezone value 'Europe/Kyiv', we selected the timezone 'UTC' for now. in /var/www/agent_stack/data/www/ajaxhispano.com/template/agent.layouts/content.php on line 61
2016-07-14 12:50:00