Comprender el concepto de los Modelos de Mezcla Gaussianos

Creo que ayudaría si primero miras lo que representa un modelo GMM. Usaré funciones de la Caja de herramientas de estadísticas , pero usted debería poder hacer lo mismo usando VLFeat.

Comencemos con el caso de una mezcla de dos distribuciones normales 1-dimensionales . Cada gaussiano está representado por un par de media y varianza. La mezcla asigna un peso a cada componente (anterior).

Por ejemplo, permite mezcle dos distribuciones normales con pesos iguales (p = [0.5; 0.5]), la primera centrada en 0 y la segunda en 5 (mu = [0; 5]), y las varianzas iguales a 1 y 2 respectivamente para la primera y segunda distribuciones (sigma = cat(3, 1, 2)).

Como puede ver a continuación, la media cambia efectivamente la distribución, mientras que la varianza determina qué tan ancha/estrecha y plana/puntiaguda es. El anterior establece las proporciones de mezcla para obtener el modelo combinado final.

% create GMM
mu = [0; 5];
sigma = cat(3, 1, 2);
p = [0.5; 0.5];
gmm = gmdistribution(mu, sigma, p);

% view PDF
ezplot(@(x) pdf(gmm,x));

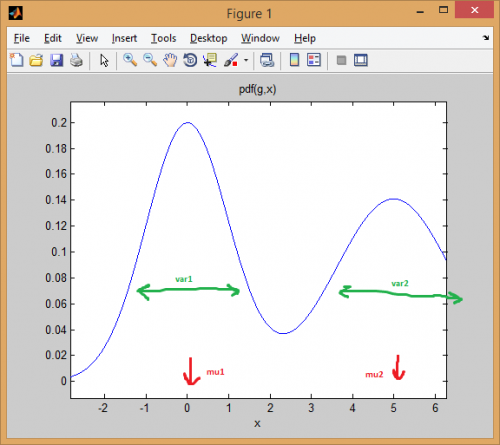
La idea de EM clustering es que cada distribución representa un clúster. Así que en el ejemplo anterior con datos unidimensionales, si se le diera una instancia x = 0.5, la asignaríamos como perteneciente al primer clúster/modo con 99.5% de probabilidad

>> x = 0.5;
>> posterior(gmm, x)
ans =
    0.9950    0.0050    % probability x came from each component

Puede ver cómo la instancia cae bien por debajo de la primera curva de campana. Mientras que si se toma un punto en el medio, la respuesta sería más ambigua (punto asignado a la clase=2 pero con mucha menos certeza):

>> x = 2.2
>> posterior(gmm, 2.2)
ans =
    0.4717    0.5283

Lo mismo los conceptos se extienden a una dimensión superior con distribuciones normales multivariantes. En más de una dimensión, la matriz de covarianza es una generalización de varianza, con el fin de tener en cuenta las interdependencias entre entidades.

Aquí hay un ejemplo de nuevo con una mezcla de dos distribuciones MVN en 2 dimensiones:

% first distribution is centered at (0,0), second at (-1,3)
mu = [0 0; 3 3];

% covariance of first is identity matrix, second diagonal
sigma = cat(3, eye(2), [5 0; 0 1]);

% again I'm using equal priors
p = [0.5; 0.5];

% build GMM
gmm = gmdistribution(mu, sigma, p);

% 2D projection
ezcontourf(@(x,y) pdf(gmm,[x y]));

% view PDF surface
ezsurfc(@(x,y) pdf(gmm,[x y]));

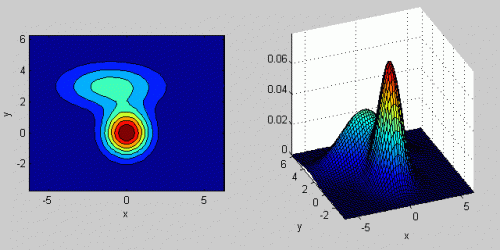
Hay cierta intuición detrás de cómo la matriz de covarianza afecta la forma de la función de densidad de la articulación. Para instancia en 2D, si la matriz es diagonal implica que las dos dimensiones no co-varían. En ese caso, el PDF se vería como una elipse alineada con el eje estirada horizontal o verticalmente de acuerdo con la dimensión que tiene la varianza más grande. Si son iguales, entonces la forma es un círculo perfecto (distribución extendida en ambas dimensiones a una tasa igual). Finalmente, si la matriz de covarianza es arbitraria (no diagonal pero aún simétrica por definición), entonces probablemente se verá como una elipse estirada girada en algún ángulo.

Así que en la figura anterior, debería ser capaz de distinguir los dos "baches" y qué distribución individual representan cada uno. Cuando vayas a dimensiones 3D y superiores, piensa en el it como representando (hiper-)elipsoides en N-dims.

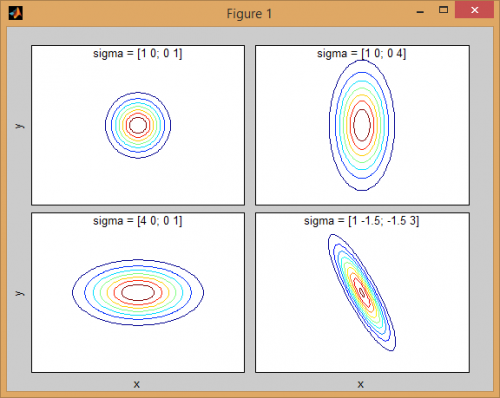
Ahora cuando se está realizando clustering utilizando GMM, el objetivo es encontrar los parámetros del modelo (media y covarianza de cada distribución, así como la antecedentes) para que el modelo resultante se ajuste mejor a los datos. La estimación de mejor ajuste se traduce en maximizando la probabilidad de los datos dados el modelo GMM (lo que significa que elige el modelo que maximiza Pr(data|model)).

Como otros han explicado, esto se resuelve iterativamente usando el algoritmo EM; EM comienza con una estimación inicial o conjetura de los parámetros del modelo de mezcla. Iterativamente re-puntúa las instancias de datos contra la densidad de mezcla producida por el parámetros. Las instancias re-puntuadas se utilizan para actualizar las estimaciones de parámetros. Esto se repite hasta que el algoritmo converge.

Desafortunadamente, el algoritmo EM es muy sensible a la inicialización del modelo, por lo que podría tomar mucho tiempo converger si establece valores iniciales pobres, o incluso quedarse atascado en local optima. Una mejor manera de iniciar los parámetros GMM es usar K-means como primer paso (como has mostrado en tu código), y usando la media / cov de esos clusters para inicializar EM.

Al igual que con otras técnicas de análisis de clústeres, primero necesitamos decidir el número de clústeres a utilizar. La validación cruzada es una forma sólida de encontrar una buena estimación del número de clusters.

EM clustering sufre del hecho de que hay muchos parámetros para encajar, y generalmente requiere muchos datos y muchas iteraciones para obtener buenos resultados. Un modelo sin restricciones con mezclas M y datos dimensionales D implica el ajuste D*D*M + D*M + M parámetros (M matrices de covarianza cada una de tamaño DxD, más M vectores medios de longitud D, más un vector de priores de longitud M). Eso podría ser un problema para conjuntos de datos con gran número de dimensiones. Por lo tanto, es costumbre imponer restricciones y suposiciones para simplificar el problema (una especie de regularización para evitar problemas de sobreajuste). Por ejemplo, podría fijar la matriz de covarianza para que sea solo diagonal o incluso tener las matrices de covarianza compartido entre todos los gaussianos.

Finalmente, una vez que haya ajustado el modelo de mezcla, puede explorar los clústeres computando la probabilidad posterior de las instancias de datos utilizando cada componente de mezcla (como he mostrado con el ejemplo 1D). GMM asigna cada instancia a un clúster de acuerdo con esta probabilidad de "pertenencia".

Aquí hay un ejemplo más completo de clustering de datos usando modelos de mezcla gaussianos:

% load Fisher Iris dataset
load fisheriris

% project it down to 2 dimensions for the sake of visualization
[~,data] = pca(meas,'NumComponents',2);
mn = min(data); mx = max(data);
D = size(data,2);    % data dimension    

% inital kmeans step used to initialize EM
K = 3;               % number of mixtures/clusters
cInd = kmeans(data, K, 'EmptyAction','singleton');

% fit a GMM model
gmm = fitgmdist(data, K, 'Options',statset('MaxIter',1000), ...
    'CovType','full', 'SharedCov',false, 'Regularize',0.01, 'Start',cInd);

% means, covariances, and mixing-weights
mu = gmm.mu;
sigma = gmm.Sigma;
p = gmm.PComponents;

% cluster and posterior probablity of each instance
% note that: [~,clustIdx] = max(p,[],2)
[clustInd,~,p] = cluster(gmm, data);
tabulate(clustInd)

% plot data, clustering of the entire domain, and the GMM contours
clrLite = [1 0.6 0.6 ; 0.6 1 0.6 ; 0.6 0.6 1];
clrDark = [0.7 0 0 ; 0 0.7 0 ; 0 0 0.7];
[X,Y] = meshgrid(linspace(mn(1),mx(1),50), linspace(mn(2),mx(2),50));
C = cluster(gmm, [X(:) Y(:)]);
image(X(:), Y(:), reshape(C,size(X))), hold on
gscatter(data(:,1), data(:,2), species, clrDark)
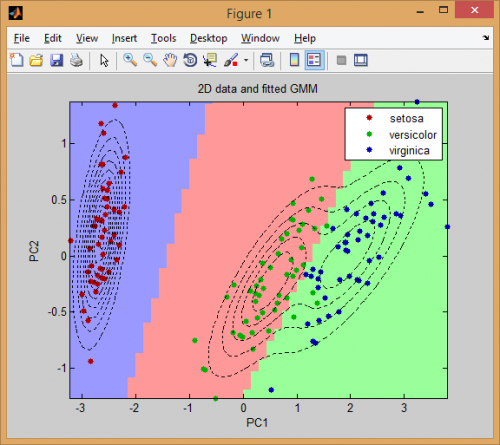
h = ezcontour(@(x,y)pdf(gmm,[x y]), [mn(1) mx(1) mn(2) mx(2)]);
set(h, 'LineColor','k', 'LineStyle',':')
hold off, axis xy, colormap(clrLite)
title('2D data and fitted GMM'), xlabel('PC1'), ylabel('PC2')